[선형대수]미적분

미분

: 최적화를 하기 위해서는 입력값이 변했을 때 함수의 출력값이 어떻게 달라지는지를 정량적으로 알아야 함

함수의 그래프상에 있는 한 점을 줌심으로 그래프를 무한히 확대해 보면 그래프의 모양이 직선에 가까워지는데 이때의 기울기를 미분이라고 한다. 이 직선은 같은 점을 기준으로 그린 그래프의 접선과 같다.

 

신명망에서 미분의 필요성 : https://gggggeun.tistory.com/120 https://gggggeun.tistory.com/121

미분 개념 : https://www.youtube.com/watch?v=kMZ3RJEaLE4

 

 

접선의 방정식

• 함수 f(x)에서 x의 값을 dx만큼 변화시켰을 때 f(x)의 변화량 (f(x+dx)-f(x))는 f'(x)dx와 같다.
• 미분 : y=f(x)라는 그래프상의 점(a,f(a))가 있을 때 그 점에서 그은 접선의 기울기는 f'(a)이며 a에서의 순간 변화율을 의미
• 적분 : 도함수 f'(x)의 하방 면적은 원 함수 f(x)의 y의 값이다. ex) f(x) = x의 제곱

# scipy.misc 패키지의 derivative() 사용하여 기울기 계산
from scipy.misc import derivative
print(derivative(f, 0, dx=1e-6))
print(derivative(f, 1, dx=1e-6))

x, y = sympy.symbols('x,y')
f = x**2 + 4*x*y + 4*y**2
f

# diff() 함수로 미분. 변수, 상수를 구분하기 위하여 편미분인 것처럼 입력 변수 지정
sympy.diff(f,x)

적분

• 적분은 미분과 반대되는 개념. 부정적분과 정적분이 있다.
  • 부정적분은 정확하게 미분과 반대되는 개념. 즉 반 미분이다. 어떤 함수를 미분하여 나온 결과인 도함수라고 가정하고 이 도함수에 대한 미분되기 전의 원래의 함수를 찾는 과정 또는 그 결과를 의미
  • 정적분은 독립변수 x가 어떤 구간 [a,b] 사이일 때 그 구간에서 함수 f(x)의 값과 수평선(x축)이 이루는 면적을 구하는 행위 혹은 그 값을 의미

적분의 개념 : https://www.youtube.com/watch?v=kV2j3S5qBm4

미분과 적분의 관계 : https://www.youtube.com/watch?v=xAAAvj7bmKQ

 

x,y = sympy.symbols('x y')
f = 2*x+y
f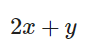

sympy.integrate(f,x)

정적분은 심파이 등으로 부정적분을 구한 뒤 미적분학의 기본 정리를 사용하여 푸는 방법과 원래 함수의 면적 부분을 실제로 잘게 쪼개어 면적을 근사하게 구하는 수치적분 두가지 방법으로 구할 수 있다.

 

•  intergrate(정적분)